배낭 문제 (knapsack problem)

배낭 문제란.. 나무위키 왈 담을 수 있는 최대 무게가 정해진 배낭과 함께 각각의 무게와 가치가 주어진 아이템의 집합이 주어졌을 때, 배낭에 담은 아이템들의 가치의 합이 최대가 되도록 하는 아이템들의 부분집합을 찾는 문제라고 함.

즉 쉽게 말해서 도둑이 가방에 담을 수 있는 양이 정해져 있는데 얼마나 효율적으로 비싼 물건을 담아 최고의 이득을 볼 수 있는지.. 이런 문제이다. 

배낭문제는 크게 fractional knapsack problem, 0-1 knapsack problem 로 나눌 수 있다!

 

 

 

1. fractional knapsack problem (분할 가능한 배낭문제)

 이 유형은 좀 단순하다고 생각된다. 별 다른 제약 없이 짐이 분할이 가능한 것이다. 

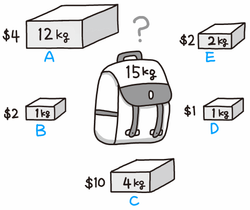
무슨말이냐면, 위 사진과 같이 짐이 있을떄, A에서 5kg만 챙기고, C에서 2kg만 챙기는게 가능하다는 것이다. 이 경우에는  그냥 1kg당 가치를 따져서 비싼 물건부터 챙기면 될 것이다. 

너무 단순한 내용이라 이정도만 정리 해도 될 것 같다.

 

 

 

2. 0-1 knapsack problem (분할 가능하지 않은 배낭문제)

배낭 문제의 대다수는 이 유형이다. 0-1 배낭 문제는 위 분할가능한 문제와 반대로 짐이 분할이 불가능한 것이다.

예를 들어, 위 사진과 같은 상황에서 짐을 자르거나 일부만 챙기지 못하고, A를 챙기려면 무조건 12kg을 다 챙겨야한다! 그러므로 짐을 고르는 조합을 고려해보고 그 중 가치가 높은 것을 선택하면 될 것이다.

 

- 우선 brute forcing 으로 해결해볼 수 있다. 가능한 모든 짐 조합 경우의 수를 생각해보고 그 중 가치가 제일 높은 것을 고르면 될 것. 그렇지만 시간이 너무 오래 걸릴 것이다. 짐이 n개라면 가능한 조합의 수가 2^n개... 그렇다면 최악의 경우 시간복잡도가 O(2^n)....?? 

 

- 그 다음 방안으로는 Dynamic Programming (DP)을 생각해볼 수 있다. DP는 항상 점화식을 생각하는게 너무 어렵다... 

 

우선 내가 생각한 건 일차원 배열을 이용하는 것이다. 

우선 dp[배낭에 넣을 수 있는 최대 무게]를 생각한다. dp[n]의 값은, nkg만큼의 짐을 담을 수 있는 배낭에 담을 수 있는 최대 가치? 라고 생각했다. 짐을 하나씩 넣어보면서 최대 가치로 값을 업데이트할 것이다. 모든 짐을 생각해보고 마지막에 dp[배낭에 넣을 수 있는 최대 무게] 에 저장된 값이 최대 가치일 것이다.

값을 업데이트 할 떄는 max(dp[ i ], dp[ i - 짐의 무게] + 짐의 가치) 가 될 것.

 

이렇게 말로 설명하면 너무 복잡해보여서 백준 문제로 예시를 들어보겠다. (백준 12865 C++)

https://www.acmicpc.net/problem/12865

12865번: 평범한 배낭

위 문제의 예제를 보자. 7kg의 배낭에 6kg $13, 4kg $8, 3kg $6, 5kg $12의 짐을 챙길 것이다.

우선 이런 dp배열을 선언!

 

그 다음 짐을 하나씩 넣어보면서 배열에 접근할 것이다. 우선 6kg $13로 생각을 했다. 

 

여기서 주의할 점은 dp[7]부터 dp[1]까지 차례로 생각해야된다는 것! 그 이유는 생각해보면 단순하다. dp[7]을 생각할 때 dp[1]~dp[6]을 고려할 것이므로 먼저 dp[1]~dp[6]을 업데이트 한 후 dp[7]을 고려하면 해당 짐이 여러번 반영될 수 있다. (당연한 소리..)

우선 dp[7]을 생각해보자. 7kg을 담을 수 있는 배낭에 첫번째 짐을 넣는것. 6kg을 넣을 수 있고 0<13이므로 최대 가치는 13이 되는 것이다. 6kg 배낭에도 넣을 수 있으므로 dp[6]도 업데이트 되었다.

 

그 다음 짐 4kg $8 를 생각해보자.

마찬가지로 dp[7]부터 생각했다. dp[7]을 업데이트 할때 max(dp[7], dp[7-4] + 8)인 이유는... max(이번 짐 포함 X 최대 가치, 이번 짐 포함 최대 가치) 인 것이다. 

 

그 다음 짐을 생각해보면 다음과 같이 된다. (3kg $6)

이렇게 계속 하면 된다...!

 

#include <iostream>

using namespace std;
typedef long long ll;
ll n, total_wei;
ll wei, val;
ll dp[100'010];

int main(void) {
	ios_base::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin >> n >> total_wei;

	for (ll i = 0; i < n; i++) {
		cin >> wei >> val;
		for(ll j = total_wei; j > 0; j--){
			if(wei <= j) dp[j] = max(dp[j], dp[j - wei] + val);
		}
	}

	cout << dp[total_wei];
}

 

다른 분들의 블로그글들을 보니 다들 이차원 배열로 구현하셨음. 그치만 남의 글 보는 거 넘무 머리아파...